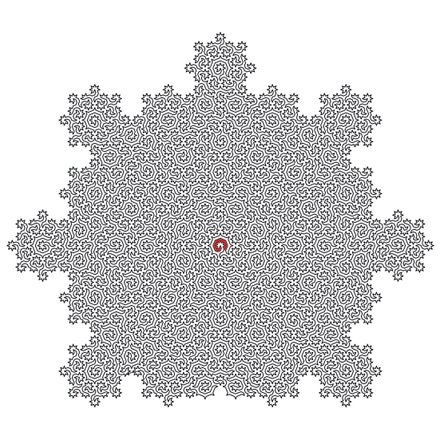
При создании дьявольского лабиринта исследователи вдохновлялись принципами фрактальной геометрии — так называемыми гамильтоновыми циклами, формирующими очень запутанный и недружелюбный узор. Такие системы имеют огромный потенциал к масштабированию без повторений, сохраняя максимальную сложность на всех участках пути.
Ярким примером гамильтонова цикла служит задача о ходе коня, для выполнения которой игроку необходимо однократно посетить соответствующей фигурой каждую клетку шахматной доски. В данном случае каждый маршрут коня, проходящий через все клетки доски только один раз, представляет собой гамильтонов путь — по этому же принципу формировался и фрактальный лабиринт британских ученых.

Исследователи отмечают, что конструкция лабиринта во многом напоминает атомарную структуру квазикристаллов — эти образования имеют упорядоченную, но апериодическую структуру, крайне редко встречаясь в некоторых минералах и метеоритах.
Таким образом, даже несмотря на то, что внешне части фрактального лабиринта могут выглядеть довольно однообразно, их наложение друг на друга демонстрирует уникальную структуру каждого изгиба и поворота. Эта хаотичность и непредсказуемость не позволяет выработать определенный алгоритм нахождения пути до центра — решение получится найти лишь при помощи обычного перебора возможных маршрутов.
Надеемся, что вам не придется оказаться внутри одного из этих фрактальных орнаментов вживую: их избыточная сложность и отсутствие повторяющихся участков станут настоящим адом для наблюдателя, ищущего дорогу к центру или, напротив, пытающегося выбраться на свободу.
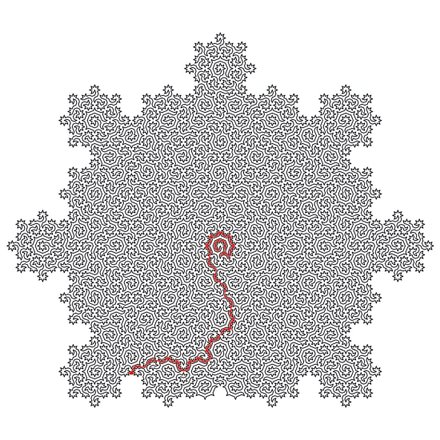
Тем не менее, в отличие от классического лабиринта (например, Кносского лабиринта), в котором единственный вход одновременно являлся и выходом, нагромождение гамильтоновых циклов имеет гораздо больше вариантов прохождения — стоит ли говорить, что они запутали бы и самого минотавра.
О древнем лабиринте, недавно обнаруженном на острове Крит, читайте в нашем материале.






